ТЕОРИЯ ПРЯМОУГОЛЬНОГО ВОЛНОВОДА
5.1 Общие сведения.
Прямоугольный волновод
(ПВ) - линия передачи СВЧ диапазона в виде металлической трубы прямоугольного сечения, заполненной однородным изотропным диэлектриком (чаще всего - воздух), рисунок 5.1. ПВ используется в сантиметровом и верхней части миллиметрового диапазонов. Для поперечных размеров ПВ приняты следующие обозначения: a - величина широкой стенки; b - величина узкой стенки, рисунок 5.1.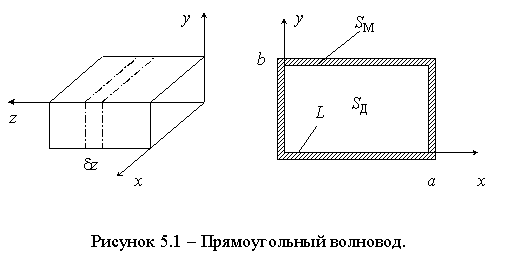
Величины
a и b принято измерять в миллиметрах. Размеры ПВ, используемых в технике СВЧ, стандартизированы. Наиболее распространенными являются сечения 23х10 мм и 8х16 мм. Основными преимуществами ПВ, которые обусловливают их широкое применение в технике СВЧ, являются:- полная помехозащищенность, т.к. ПВ является закрытой структурой, то внешние поля не проникают внутрь и поле распространяющейся в ПВ волны никак не влияет на окружающие объекты;
- малое затухание волны в ПВ;
- высокое значение пробивной мощности, что делает ПВ незаменимыми в качестве фидеров передающих антенн мощных передатчиков и радиолокационных станций.
К недостаткам ПВ следует отнести большую массу и габариты, что ограничивает возможности их использования в составе бортовой аппаратуры искусственных спутников Земли и других космических аппаратов. Однако, современные технологии позволяют изготавливать ПВ путем напыления слоя серебра на внутреннюю поверхность прямоугольной трубы, изготовленной из пластика, что существенно уменьшает массу ПВ.
5.2 Расчет полей в ПВ.
Собственными волнами
называют свободные гармонические электромагнитные волны в прямоугольном волноводе с идеально проводящими стенками, заполненном диэлектриком без потерь.5.2.1 Постановка задачи
. Для определения полей собственных волн в ПВ необходимо решить однородные уравнения Гельмгольца относительно комплексных амплитуд напряженностей электрического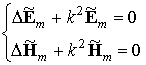 (5.1)
(5.1)
при граничных условиях на идеально проводящих стенках волновода:
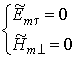 ,(5.2)
,(5.2)
где:
k - волновое число в свободном пространстве -![]() и
и ![]() - тангенциальная и нормальная составляющие комплексных амплитуд напряженностей электрического и магнитного полей.
- тангенциальная и нормальная составляющие комплексных амплитуд напряженностей электрического и магнитного полей.
В силу продольной однородности геометрических и физических параметров ПВ решение задачи (5.1)-(5.2) можно представить в виде волн, бегущих вдоль оси Oz:
 ,(5.3)
,(5.3)
где
b - постоянная распространения волны.Функции ![]() и
и ![]() описывают распределение полей в поперечном сечении ПВ. Подставив (5.3) в (5.1), получим двумерные уравнения для нахождения этих функций:
описывают распределение полей в поперечном сечении ПВ. Подставив (5.3) в (5.1), получим двумерные уравнения для нахождения этих функций:
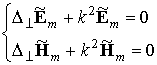 ,(5.4)
,(5.4)
где:  - двумерный оператор Лапласа;
- двумерный оператор Лапласа;
![]() - поперечное волновое число.
- поперечное волновое число.
Векторные уравнения (5.4) распадаются на скалярные уравнения для x , y и z компонент полей ![]() и
и ![]() , т.е. нахождение полей собственных волн ПВ сводится к решению 6 скалярных уравнений Гельмгольца в поперечном сечении ПВ. Для удовлетворения граничным условиям на идеально проводящих стенках необходимо знать распределения на них поверхностных зарядов и токов, однако они не известны заранее. Поэтому решение скалярных уравнений можно получить только для продольных компонент полей Emz и Hmz, т.к. они удовлетворяют простым и одинаковым на всех стенках условиям:
, т.е. нахождение полей собственных волн ПВ сводится к решению 6 скалярных уравнений Гельмгольца в поперечном сечении ПВ. Для удовлетворения граничным условиям на идеально проводящих стенках необходимо знать распределения на них поверхностных зарядов и токов, однако они не известны заранее. Поэтому решение скалярных уравнений можно получить только для продольных компонент полей Emz и Hmz, т.к. они удовлетворяют простым и одинаковым на всех стенках условиям:
![]()
![]() ,
,
где ![]() - производная по нормали к стенке волновода.
- производная по нормали к стенке волновода.
5.2.2 Классы собственных волн ПВ
. Легко убедится, что поставленные задачи для продольных компонент имеют нулевые решения: Emz=0 и Hmz=0. На основании этого выделяют два класса собственных волн ПВ: E-волны - это собственные волны ПВ, у которых имеется продольная составляющая только электрического поля Ez, а Hz=0; H-волны - это собственные волны ПВ, у которых имеется продольная составляющая Hz, а Ez=0. E-волны называют также электрическими или поперечно-магнитными волнами (ТМ-волнами). Н-волны называют, соответственно, магнитными или поперечно-электрическими. Второе название отражает тот факт, что для Е-(Н-) волн вектор магнитного (электрического) поля лежит в плоскости поперечного сечения ПВ (плоскость z=const на рисунке 5.1). Собственную волну ПВ, у которойПоперечные компоненты полей:
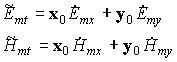
выражаются через
Emz и Hmz при помощи уравнений Максвелла: ,(5.5)
,(5.5)
где ![]() - двумерный оператор Гамильтона;
- двумерный оператор Гамильтона;
x
0, y0, z0 - орты прямоугольной системы координат.Подставив в (5.5) решение скалярного уравнения Гельмгольца для ![]() при условии
при условии ![]() мы получим выражения для поперечных компонент E-волны. Аналогично получаются выражения для поперечных компонент полей H-волны.
мы получим выражения для поперечных компонент E-волны. Аналогично получаются выражения для поперечных компонент полей H-волны.
Итак, расчет полей собственных волн ПВ сводится к решению двух задач:
E-волны: 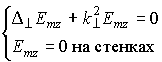
H-волны: 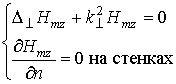
5.2.3 Типы собственных волн ПВ
. Используя метод разделения переменных, легко получить решения задач (5.6) и (5.7), удовлетворяющие граничным условиям при x=(0; a) и y=(0; b) (рисунок 5.1):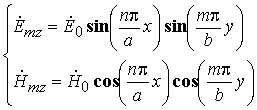 , (5.8)
, (5.8)
где ![]() и
и ![]() определяют амплитуды полей;
определяют амплитуды полей;
n
и m - целые числа.Остальные компоненты полей определяются дифференцированием
Emz или Hmz в соответствии с (5.5). Каждому набору двух целых чисел (n,m) соответствует свое распределение поля в ПВ, т.е. набор (n,m) определяет тип собственной волны в ПВ. Другими словами, существует множество типов E- и H-волн. Для них приняты следующие обозначения: Enm и Hnm.
5.3 Анализ собственных волн ПВ.
5.3.1 Возможные типы волн
. Из (5.8) следует, что для E-волн5.3.2 Постоянные распространения
. В соответствии с методом разделения переменных, решения (5.8) задач (5.6)-(5.7) получены при условии: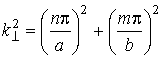 .
.
Поперечное волновое число определяется индексами
n и m, т. е. типом волны, и размерам ПВ. Следовательно, каждому типу волны соответствует своя постоянная распространения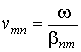 .
.
5.3.3 Затухающие волны в ПВ
. Согласно (5.3) поле в ПВ имеет вид распространяющейся волны только при действительном b, т.е. когда k>k^ . Если k<k^ , то подставив![]() .(5.9)
.(5.9)
Аналогичное выражение можно получить для магнитного поля.
Выражение (5.9) описывает поле, которое совершает синфазные гармонические колебания по закону ![]() , при этом распределение поля в поперечном сечении
, при этом распределение поля в поперечном сечении ![]() и
и ![]() по-прежнему определяется задачами (5.6) и (5.7) и уравнениями (5.5), т.е. остается тем же самым, что и у распространяющихся E- или H-волны. Поэтому такое поле называют затухающей E
по-прежнему определяется задачами (5.6) и (5.7) и уравнениями (5.5), т.е. остается тем же самым, что и у распространяющихся E- или H-волны. Поэтому такое поле называют затухающей E
5.3.4 Условия распространения волны в ПВ
. Определим условия, при которых на данной частоте в ПВ с размерами a и b будет распространяться заданный тип волны. Как было отмечено выше, распространяющаяся волна будет существовать в волноводе при выполнении неравенства k>k^ , т. е. .
.
Тогда частота должна удовлетворять неравенству:
w < w кр, где введено обозначение: .
.
w
кр называется критической частотой данного типа волны. При w < w кр волна с индексами (n, m) распространяться не будет. Критическая частота растет с увеличением индексов n и m . Волна, обладающая минимальной w кр называется основной волной (основным типом волны). Все остальные волны называют высшими типами волн.Поскольку
a - размер широкой стенки, то из выражения для w кр следует, что в ПВ основной волной будет волна с n=1, m=0. Очевидно, что это H-волна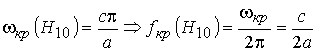 .
.
В теории волноводов используется также понятие
критической длины волны, соответствующей критической частоте в свободном пространстве: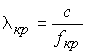 . Для волны
. Для волны На частотах, меньших критической частоты основной волны, волновой процесс в ПВ существовать не может. В данном случае волновод называют
запредельным. Поле в запредельном волноводе представляет собой суперпозицию бесконечного числа затухающих волн вида (5.8), соответствующих различным коэффициентам затухания: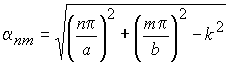 .(5.10)
.(5.10)
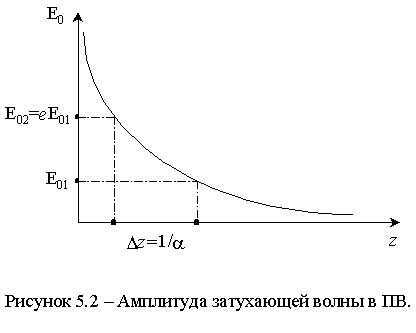
Электромагнитное поле в любом сечении, как отмечалось выше, синфазно изменяется со временем по гармоническому закону. Амплитуда колебаний очень быстро убывает с ростом
z. Отрезки запредельных волноводов часто используют в качестве аттенюаторов, т.к. вносимое ими затухание на заданной частоте легко рассчитать с помощью (5.10) и (5.9).5.3.5 Длина волны в ПВ
. Длина волны в волноводе определяется следующим образом .
.
Перейдем в правой части от длины волны к частоте:
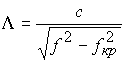 .
.
Отметим следующие особенности:
- длина волны в волноводе больше длины волны в свободном пространстве
 при той же частоте волны;
при той же частоте волны; - при
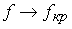
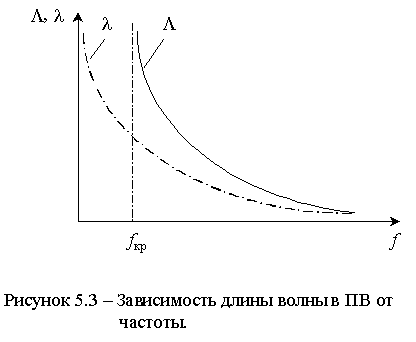
при ![]()
![]()
, т.е. с ростом частоты длины волны в волноводе приближается к длине волны в свободном пространстве - рисунок 5.3.
5.3.5 Фазовая и групповая скорости волн в ПВ
. Аналогично выражению для длины волны можно получить формулу для расчета фазовой скорости собственной волны ПВ:![]()
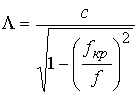 .
.
Фазовая скорость собственных волн ПВ больше скорости света, поэтому собственные волны ПВ называют быстрыми волнами. Групповая скорость собственных волн в ПВ (скорость распространения энергии) не совпадает с фазовой:
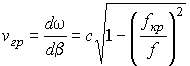 .
.
Групповая скорость меньше скорости света, при ![]()
5.4 Потери в ПВ.
В реальном ПВ происходят потери электромагнитной энергии, в результате чего наблюдается затухание волн. Этот процесс характеризуется
погонной мощностью потерь:,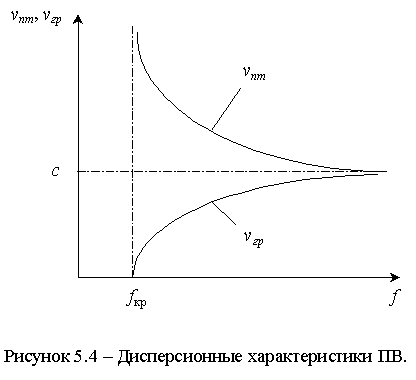
![]()
где
d P - мощность потерь в отрезке линии передачи длиной d z, рисунок 5.1.Используя общее выражение для средней мощности потерь гармонического поля, получим:
 ,(5.11)
,(5.11)
где
d V - объем ПВ, заключенный между двумя поперечными сечениями с координатами z и z+d z;S
- сечение ПВ.d
V содержит разнородные среды: металл оболочки в сечении SМ и заполняющий диэлектрик в SД (рисунок 5.1). Следовательно, интеграл по S = SМ + SД распадается на два: интеграл по SМ - определяет потери в металле, т. е. в стенках волновода, и интеграл по SД - потери в диэлектрике.5.4.1 Потери в стенках ПВ.
Так как на рабочих частотах волновода (диапазон СВЧ) наблюдается сильный поверхностный эффект, то потери в металле принято рассчитывать исходя из выражения для мощности потерь при скин-эффекте. Тогда погонная мощность потерь примет вид: ,(5.12)
,(5.12)
где
d S - внутренняя поверхность оболочки отрезка ПВ длиной d z;L
- внутренний контур сечения оболочки ПВ (рисунок 5.1);s
- удельная проводимость материала оболочки;D
- глубина проникновения поля (толщина скин-слоя);Hm
t - касательная к d S компонента магнитного поля волны в ПВ.Выражение (5.12) намного удобнее для практических расчетов, чем (5.11), так как содержит одномерный интеграл и более простое подынтегральное выражение.
Hm
t - компонента поля волны в ПВ со стенками из реального металла с конечной проводимостью s . Эта волна уже не будет являться собственной волной ПВ. Нахождение ее электромагнитного поля - весьма сложная задача. Однако в реальной ситуации потери в стенках волновода малы, поэтому при расчетах погонной мощности потерь в металле в качестве хорошего приближения для Hmt можно использовать известные выражения для магнитных полей собственных волн структуры. Обычно реальный волновод работает в одномодовом диапазоне, тогда его поле можно приближенно считать совпадающим с полем основной волны Н10. Подставив выражение для Hmz при n=1, m=0 из (5.8) в формулу для поперечных компонентов магнитного поля (5.5), после дифференцирования получим: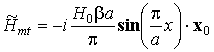 ,
,
для упрощения формул мы рассматривает сечение ПВ с координатой
z=0. Полное магнитное поле волны Н10 примет вид: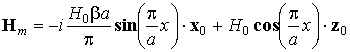 .
.
На боковых стенках (
x=0; a) имеем: .
.
Таким образом, достаточно проинтегрировать в (5.12) по двум стенкам
x=0 и y=0 и результат удвоить: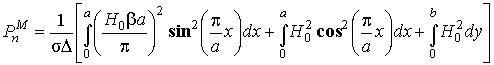 .
.
Вычислив элементарные интегралы, получим выражение для погонных потерь в стенках волновода для основной волны:
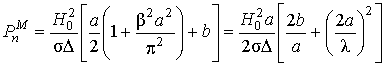 ,(5.13)
,(5.13)
где
l - длина волны в свободном пространстве при рабочей частоте - так называемая рабочая длина волны: 2a/l = f/fкр.5.4.2 Потери в диэлектрике
. На практике потери в диэлектрике определяют по формуле (5.11), интегрируя по SД. Магнитные потери в диэлектрике намного меньше диэлектрических, поэтому ими обычно пренебрегают: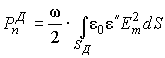 .
.
Процедура расчета аналогична изложенной в предыдущем параграфе. Вместо реального поля в волноводе с потерями подставляется выражение для поля собственной волны и проводится интегрирование.
5.4.3
Коэффициент затухания ПВ. При наличии потерь волна в направляющей структуре будет затухать Ее амплитуда уменьшается вдоль ПВ по закону e-a z - как изображено на рисунке 5.2, однако в данном случае затухание обусловлено рассеянием электромагнитной энергии. Коэффициент затухания имеет тот же смысл, что и в п. 5.3.3. Если P - передаваемая вдоль волновода мощность, то легко показать, что коэффициент затухания:![]() ,(5.14)
,(5.14)
Мощность
P на входе волновода с потерями равна мощности генератора.