ТЕОРИЯ ИЗМЕРИТЕЛЬНОЙ ЛИНИИ
1.1 Электромагнитное поле в измерительной линии.
Измерительная линия представляет собой отрезок продольно-однородной линии передачи (ЛП) с введенных в нее зондом – металлическим штырем, ориентированным вдоль силовых линий электрического поля.
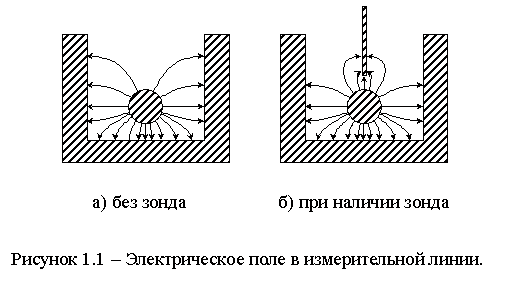
Введение зонда в линию нарушает ее однородность и приводит к искажению исследуемой картины распределения электромагнитного поля – рисунок 1.1 и появлению в измерительной линии отраженной от зонда волны. Это влечет за собой ошибки в определении координат каретки. Однако ошибка будет минимальной в точках минимума амплитуды колебаний. Поэтому измерения в линии, работающей на конечную нагрузку, производят вблизи минимумов. В узлах стоячей волны напряженность электрического поля равна нулю и искажения отсутствуют. Их координаты определяются точно, поэтому узлы всегда используются в качестве опорных точек при работе с измерительной линией.
Действие зонда можно описать введением в линию эквивалентной комплексной шунтирующей проводимости:
GЭ+iYЭ. Реактивная проводимость YЭ обусловлена отражением от зонда, активная проводимость представляет поглощенную зондом мощность, GЭ возрастает с увеличением глубины погружения зонда. Для устранения отражения – согласования зонда с линией передачи используется перестраиваемый резонатор, с помощью которого компенсируется реактивная проводимость зонда. Настройка резонатора осуществляется вращением шайбы и перемещением плунжера на его поверхности до достижения максимального показания гальванометра. Активная проводимость GЭ вносит ошибку в определение картины стоячей волны, поэтому выбираемая глубина погружения зонда представляет компромисс между достаточной для измерения величиной выпрямленного детектором сигнала и допустимой погрешностью измерений.
1.2 Опорная плоскость (ОП) и длина волны.
ОП - это место включения нагрузки, перенесенное в область перемещения каретки, где можно определять координаты зонда. Сопротивление в ОП (отношение напряжения к току
U/I) будет таким же, как на нагрузке, т.к. амплитуды тока и напряжения изменяются вдоль линии по периодическому закону. Для определения ОП в качестве нагрузки включают короткозамыкатель (при этом в месте включения нагрузки электрическое поле равно нулю – узел напряжения), и находят координату ближайшего к нагрузке узла.Из-за ограниченной чувствительности индикатора нельзя точно определить координату узла. Необходимо воспользоваться методом "вилки" – рисунок 1.2. Определяются координаты зонда
x1, x2 слева и справа от узла, при которых показание индикатора I1 в 3-5 раз превышают его чувствительность. Тогда координата опорной плоскости xОП определяется как среднее арифметическое:![]() .
.
Аналогично определяется координата следующего узла. Расстояние между ними будет равно половине
длины волны в линии – рисунок 1.2.
Коэффициент стоячей волны (КСВ) определяется как отношение максимальной амплитуды колебаний напряжения в линии к минимальной:
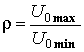 .
.
Однако реально измеряется ток в цепи детектора измерительной головки
Iд, который связан с напряжением в линии некоторой нелинейной зависимостью:![]() .
.
Калибровка заключается в нахождении этой функциональной зависимости, дающей возможность определить КСВ по измеренным значениям
Iд в максимуме и минимуме. Для диода наиболее точно функцию![]() ,
,
тогда задача калибровки детектора сводится к нахождению показателя степени
n.Калибровка производится при коротком замыкании, когда в линии существует чисто стоячая волна. При этом амплитуда напряжения изменяется по гармоническому закону:
![]() .
.
Калибровку можно осуществить двумя методами.
1.3.1 1-й метод калибровки.
Для стоячей волны ток детектора выражается следующим образом:![]() , (1.1)
, (1.1)
где А – некоторая константа. Прологарифмируем уравнение (1.1):
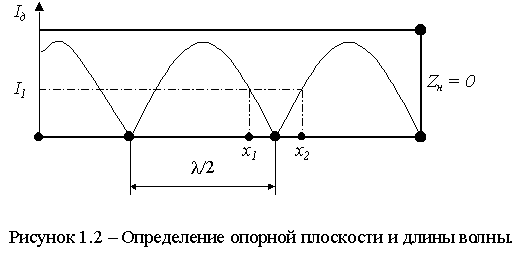
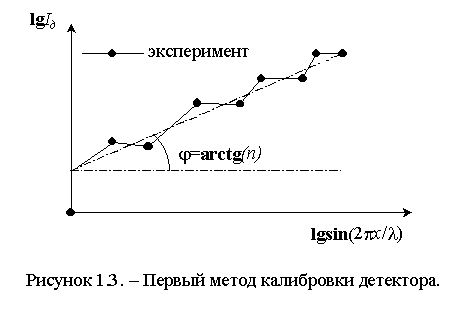
График зависимости
Из уравнения (1.2) получаем:
n = tgj . По экспериментальному графику легко определить tgj – рисунок 1.3.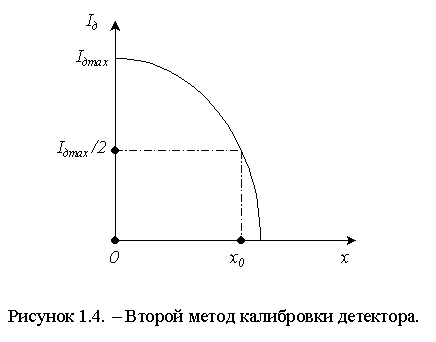
1.3.2 2-й метод калибровки. Этот метод основан на исследовании поля вблизи максимума. Необходимо измерить длину волны и расстояние x0 от сечения, в котором ток детектора максимален (Iдmax), до сечения, где ток равен половине Iдmax – рисунок 1.4.
Из (1.1) следует, что максимальный ток детектора
Iдmax = (AU0)n. При смещении на расстояние x0 он уменьшается в два раза, тогда справедливы следующие соотношения: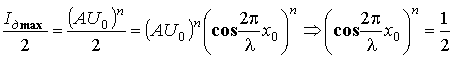 .
.
Прологарифмировав последнее уравнение легко получить выражения для показателя степени
n: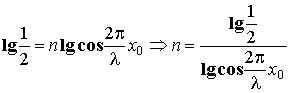 .
.
Отметим, что второй метод калибровки менее трудоемкий, чем первый. Однако он дает менее точный результат, поскольку основан на измерениях всего в двух точках и эти измерения проводятся вблизи максимума, где зонд вносит наибольшую погрешность.
1.4 Измерение КСВ.
Способ определения КВС по измеренным величинам зависит от его величины, т.е. степени рассогласования в линии. По величине КСВ классифицируется следующим образом:
- очень малый – 1<
Измерения очень малых КСВ проводят в метрологических лабораториях с применением специальных методик – при поверке и настройке измерительной аппаратуры.
1.4.1
Малый КСВ определяется методом максимума-минимума. Измеряются значения тока детектора в максимуме и минимуме поля: Iдmax , Iдmin. Необходимо, чтобы детектор был калиброван, т.е. известно n. Тогда КСВ рассчитывают по формуле: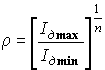 (1.3)
(1.3)
При малых сигналах полупроводниковый детектор является квадратичным, т.е.
n=2. Тогда (1.3) примет вид: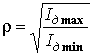 .
.
Расчеты по этой формуле можно проводить только для таких величин тока детектора, при которых его можно считать квадратичным – т.е. лежащих в области квадратичности. В этой области (при
n=2) из (1.1) вытекает следующее соотношение для стоячей волны в линии:![]() .
.
1.4.2 Определение области квадратичности детектора
основано на этом равенстве. Экспериментально снимается зависимость тока детектора от координаты вдоль линии при коротком замыкании (аналогично первому методу калибровки детектора). Измерение необходимо начать в узле стоячей волны – в области малых сигналов. По измеренным величинам рассчитывается и строится зависимость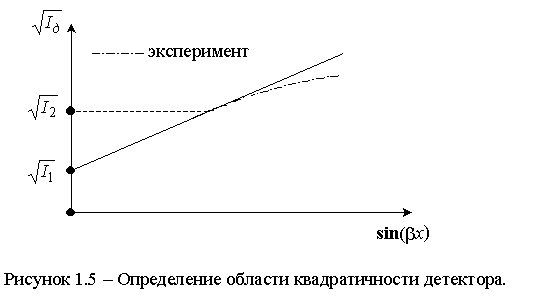
Для больших и очень больших КСВ формула (1.3) теряет смысл из-за того, что показатель степени
n зависит от величины напряжения U. При большой разнице между максимальной амплитудой колебаний напряжения в линии U0max и минимальной U0min пренебрегать этой зависимостью нельзя: показатели степени в максимуме и минимуме сильно отличаются.1.4.3 Большой КСВ
определяют по результатам исследования поля вблизи минимума. Измеряемые токи детектора должны принадлежать области квадратичности. При наличии отражения (режим рассогласования) поле в линии, как известно, представляет собой наложение бегущей и стоячей волн:Um(x) = (U
пад–Uотр)e-ib x + 2Uотрcosb x = (Uпад+Uотр)cosb x - i(Uпад–Uотр)sinb x,где
Uпад и Uотр – амплитуды падающей и отраженной волн.Амплитуда колебаний напряжения будет распределяться вдоль линии по закону:
U0(x) = |Um(x)| =![]()
Тогда, при квадратичном детекторе, ток
Iд в режиме рассогласования определяется выражением:I
д = (Uпад+Uотр)2cos2b x + (Uпад–Uотр)2sin2b x.В дальнейшем будет удобно отсчитывать расстояние
x от минимума. Для этого в данном выражении необходимо сделать замену переменной x ® x - l / 4. Тогда:I
д = (Uпад+Uотр)2sin2b x + (Uпад–Uотр)2cos2b x. (1.4)Для определения большого КСВ измеряют длину волны и расстояние
x0 между сечением линии, в котором ток детектора минимален – Iдmin и сечением, в котором он равен 2Iдmin – рисунок 1.6.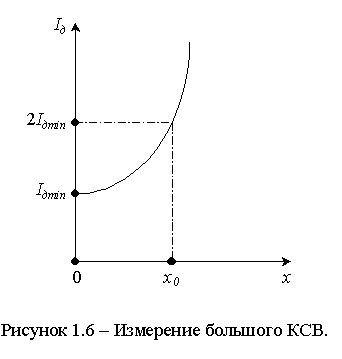
Из (1.4) следует, что Iдmin = (Uпад-Uотр)2 и:
2I
дmin = 2(Uпад-Uотр)2 = (Uпад+Uотр)2sin2b x0 + (Uпад–Uотр)2cos2b x0.Разделив последнее равенство на
(Uпад–Uотр)2 и учитывая, что КСВ: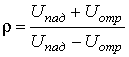 ,(1.5)
,(1.5)
получим выражение для расчета КСВ по измеренному расстоянию
x0: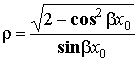 .
.
1.4.4 Очень большой КСВ
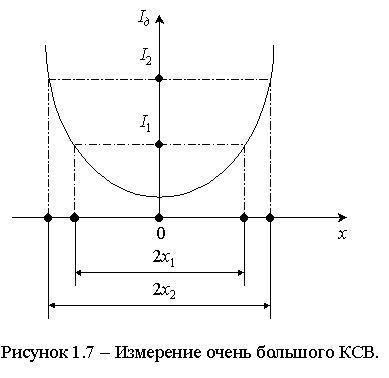
нельзя определить изложенным выше методом, т.к. при сильном рассогласовании минимум настолько мал, что величина Iдmin лежит за пределами чувствительности индикатора, т.е. не может быть измерена. В таких случаях вблизи минимума измеряют два произвольных значения тока I1 и I2, лежащих в области квадратичности детектора, длины соответствующих им хорд 2x1 и 2x2 – рисунок 1.7 и длину волны.Из (1.4), с учетом (1.5), следует, что отношение величин измеренных токов определяется выражением:
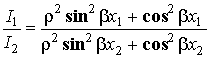 ,
,
откуда легко выразить КСВ:
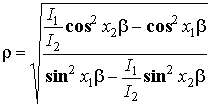
.
- Полное сопротивление нагрузки.
Используя приведенные выше методики можно измерить все вспомогательные величины, по которым определяется сопротивление нагрузки. Итак, в процессе эксперимента при коротком замыкании определяется положение опорной плоскости и длина волны в линии –
- коэффициент стоячей волны –
Действительная и мнимая части полного сопротивления нагрузки
Zн=Rн+iXн рассчитываются по формулам: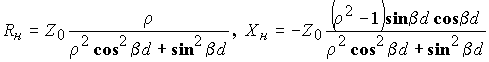 ,
,
где
Z0=50 Ом – волновое сопротивление измерительной линии.